И

ПРОБЛЕМА ЧЕТЫРЕХ КРАСОК

    Еще одной проблемой, связанной с теоремой Эйлера, является проблема четырех красок, имеющая почти 150-летнюю историю.
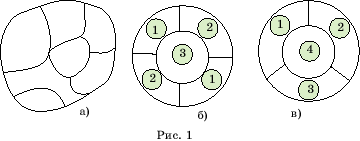
    Задача заключается в том, чтобы раскрасить данную географическую карту (рис. 1,а) так, чтобы пограничные страны были окрашены в разные цвета (не пограничные страны можно окрашивать одним цветом), использовав при этом наименьшее число красок.
    На рисунке 1,б изображена карта, для раскраски которой требуется три цвета. На рисунке 1,в изображена карта, для раскраски которой трех цветов недостаточно и требуется четыре цвета.

    В 1850 году шотландский физик Фредерик Гутри обратил внимание на то, что задачи раскрашивания карт очень популярны среди студентов-математиков в Лондоне, а сформулировал проблему четырех красок его брат Фрэнсис Гутри, который, раскрасив карту графств Англии четырьмя цветами, выдвинул гипотезу о том, что этого количества цветов достаточно для раскраски любой карты. Он привлек к проблеме внимание своего преподавателя математики А. Де Моргана, а тот сообщил о ней своему другу В. Гамильтону и тем самым способствовал ее широкому распространению.
    Однако годом рождения проблемы четырех красок считается 1878 год (в некоторых изданиях указывается 1879). Именно тогда на одном из заседаний Британского географического общества выдающийся английский математик А. Кэли четко сформулировал поставленную задачу: "Доказать, что любую географическую карту на плоскости (или на глобусе) можно правильно закрасить четырьмя красками". Раскраска карты называется правильной, если любые две страны, имеющие на карте общую границу, окрашены в различные цвета. Именно с этого момента проблема привлекла к себе внимание многих крупных математиков.
    В 1890 году английский математик П. Хивуд доказал, что любую карту на плоскости можно раскрасить в пять цветов. Однако долгое время проблема четырех красок не поддавалась решению. В 1968 году американские математики Оре и Стемпл показали, что любую карту, имеющую не более 40 стран, можно раскрасить в четыре цвета.
    В настоящее время для решения этой проблемы существенно используются компьютеры, что связано с выполнением огромного количества вычислений. В 1976 году американскими учеными К. Аппелем и В. Хакеном было получено первое машинное решение. С помощью машины они просматривали различные типы карт, и для каждого из них машина решала, может ли в данном типе найтись карта, которая не раскрашивается в четыре цвета. Учеными было просмотрено почти 2000 типов карт, и для всех был получен ответ: "Нет", - что и позволило объявить о машинном решении проблемы четырех красок.
    Теорема. (О двух красках.) Всякую карту, образованную прямыми, можно раскрасить в два цвета.
    Доказательство. Ясно, что карту, образованную одной прямой можно раскрасить в два цвета (рис. 2,а). Докажем, что если карта, образованная прямыми, раскрашена в два цвета, то карта, полученная из нее добавлением новой прямой также может быть раскрашена в два цвета (рис. 2,б).

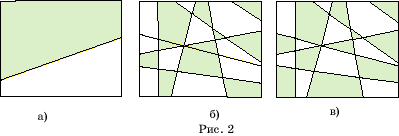    Действительно, новая прямая делит раскрашенную карту на две карты, каждая из которых раскрашена в два цвета. Причем к самой прямой примыкают пары областей, закрашенные в один цвет. Перекрасим одну из карт-половинок (безразлично, какую именно), изменив цвет каждой области на противоположный. Получим раскраску в два цвета всей карты (рис. 2,в). Поскольку любую карту, образованную прямыми можно получить последовательным добавлением прямых, то всякая такая карта может быть раскрашена в два цвета.
    Аналогично, любую карту, образованную окружностями, можно раскрасить в два цвета.
    Теорема*. (О пяти красках.) Любую карту на плоскости можно раскрасить пятью красками.
    Доказательство. Пусть дана карта на плоскости. Как и в случае задачи о трех домиках и трех колодцах, добавим к карте еще одну страну – внешнюю область. Ясно, что если мы сможем раскрасить полученную карту, то, убрав внешнюю область, получим раскраску исходной карты. Дополнительно можно предполагать, что в каждой вершине карты сходятся ровно три ребра. Действительно, если в каких-нибудь вершинах сходится большее число ребер, то проведем небольшие окружности с центрами в этих вершинах и образуем новую карту, в которой вместо вершин появятся новые страны в форме кругов. Причем число ребер, сходящихся в каждой вершине такой карты, уже будет равно трем. Если удастся раскрасить эту новую карту, то, убрав страны в форме кругов, мы получим раскраску исходной карты.
    Используя теорему Эйлера, покажем, что для карты, в вершинах которой сходится по три ребра, существует страна с числом ребер, меньшим или равным пяти.
    Обозначим через Г_nчисло стран в такой карте с числом ребер, равным n. Тогда общее число стран Г выражается формулой Г = Г₂ + Г₃ +… . (1) Обозначим через Р общее число ребер и через В общее число вершин в карте. Тогда, поскольку у каждого ребра две вершины и в каждой вершине сходятся три ребра, имеет место формула 2Р = 3В. (2) Далее, поскольку каждое ребро ограничивает две страны (в качестве страны включена внешняя область), то имеет место формула 2Р = 2 Г₂ + 3Г₃+ … . (3) Из формулы Эйлера следует равенство В – Р + Г = 2 или 6В - 6 Р + 6 Г = 12. (4)     Выразим В через Р по формуле (2), Р через Г₂, Г₃, … по формуле (3) и Г через Г₂, Г₃, … по формуле (1). Подставляя эти выражения в формулу (4), получим равенство 6Г₂ + 6Г₃ + … -(2Г₂ + 3Г₃ + … ) =12 или 4Г₂ + 3Г₃ + 2Г₄ + Г₅ + 0Г₆ – Г₇ - … = 12.     Так как вся сумма в левой части последнего равенства положительна, а все слагаемые в ней, начиная с шестого, отрицательны, то среди чисел Г₂, Г₃, Г₄, Г₅, обязательно должно найтись хотя бы одно отличное от нуля. Следовательно, существует страна с числом ребер, меньшим или равным пяти.
    Приступим теперь непосредственно к доказательству теоремы, которое будем проводить индукцией по числу стран.
    Если карта состоит из одной страны, то очевидно, для ее раскраски требуется одна краска.
    Предположим, мы доказали, что любую карту, состоящую не более чем из n стран, можно раскрасить пятью красками. Рассмотрим карту из n+1 страны, и покажем, что ее также можно раскрасить пятью красками.
    В силу сказанного выше, можно предполагать, что в каждой вершине карты сходится три ребра и существует страна С с числом ребер, меньшим или равным пяти. Возможны следующие случаи.
    Случай 1. Страна С имеет два ребра, граничащие с двумя странами С₁ и С₂ (рис. 3,а).
    Удалим общую границу между странами С и С₁. Получим карту, в которой вместо стран С и С₁ имеется одна страна С’ (рис. 3,б). По предположению индукции эту карту можно раскрасить пятью красками. Если при этом страна С’ покрашена краской № 1, а страна С₂ – краской № 2, то восстанавливая прежнюю границу и перекрашавая в исходной карте страну С любой из оставшихся красок - № 3, № 4 или № 5, получим требуемую раскраску нашей карты.

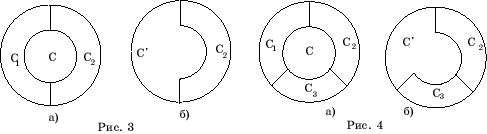    Случай 2. Страна С имеет три ребра, граничащие с тремя странами.
    Доказательство этого случая аналогично предыдущему и опирается на рисунки 4,а,б.
    Случай 3. Страна С имеет четыре ребра, граничащие с четырьмя странами.
    Если разные ребра страны С являются границами разных стран, то поступаем так же, как и в предыдущем случае (рис. 5,а,б). Однако может случится, что два противоположных ребра страны С являются границами одной и той же страны. В этом случае два соседних ребра не могут быть границами одной страны, и, следовательно, одно из этих ребер можно удалить и далее поступать как и в предыдущих случаях.

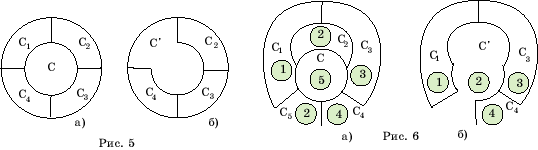    Случай 4. Страна С имеет пять ребер. Граничащие с С страны обозначим соответственно С₁, С₂, С₃, С₄, С_5.
    Среди этих стран всегда найдутся две не граничащие друг с другом (рис. 6,а). Действительно, если страны С₁ и С₃ граничат друг с другом, то страна С₂ не может граничить ни с С₄ни с С₅. Удалим два ребра страны С, граничащие с такими странами (рис. 6,б). Полученная карта будет содержать n – 2 страны. Если она раскрашена, как показано на рисунке 6,б, то исходную карту раскрашиваем согласно рисунку 6,а.
    Таким образом, мы рассмотрели все случаи и в каждом из них убедились в возможности раскраски карты. Что и завершает доказательство.
    Для раскрашивания карт специального вида может требоваться меньшее число красок.

    Задачи
    1. Раскрасьте карту, изображенную на рисунке 1,а. Какое минимальное число красок для этого потребуется?
    2. Сколько красок достаточно взять, чтобы раскрасить карту, образованную двумя концентрическими окружностями, имеющими n перегородок (рис. 1,б,в)?
    3. Докажите, что всевозможные карты на плоскости, образованные окружностями, могут быть раскрашены в два цвета.
    4. Исследуйте вопрос о том, какие свойства прямых и окружностей используются при раскрашивании карт двумя цветами. Можно ли раскрасить двумя цветами карту, образованную: а) параболами; б) эллипсами?
    5. Докажите, что если карту, заполняющую всю плоскость, можно раскрасить в два цвета, то она имеет вершины только четного индекса.
    6. Используя то, что любую карту на плоскости можно раскрасить в четыре цвета, решите задачу известного астронома и геометра Августа Мебиуса, сформулированную им в 1840 году: на плоскости нельзя начертить пять областей так, чтобы каждые две из них имели общую границу.
    7. Какое наибольшее число клеток в квадрате n x n, нарисованном на клечатой бумаге, можно закрасить так, чтобы ни в одном квадрате 2 x 2 не оказалось трех закрашенных клеток.
    8. Можно ли закрасить на клеточной бумаге 25 клеток так, чтобы у каждой из них было нечетное число закрашенных соседей? (Соседними считаются клетки, у которых есть общая сторона.)
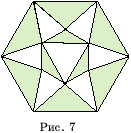
    9. На рисунке 7 изображена карта, раскрашенная в два цвета, полученная разбиением шестиугольника на треугольники. Причем треугольники, примыкающие к сторонам шестиугольника, закрашены в один цвет. Докажите, что карту, полученную разбиением 10-угольника на треугольники, нельзя раскрасить в два цвета так, чтобы треугольники, примыкающие к сторонам 10-угольника были закрашены в один цвет.

10. Сколько красок потребуется для раскраски поверхности куба, при которой соседние грани имели бы разные цвета?

    Литература
    1. Барр Ст. Россыпи головоломок. – М.: Мир, 1987.
    2. Болл У., Коксетер Г. Математические эссе и развлечения. – М.: Мир, 1986.
    3. Болтянский В.Г., Ефремович В.А. Наглядная топология. – М.: Наука, 1982 /Библиотечка “Квант”, выпуск 21.
    4. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1971.
   ^{5. Дынкин Е.Б. и др. Математические задачи. – М.: Наука, 1971 /Библиотечка
физико-математической школы, выпуск 1}^*^.
    6. Кокстер Г.С.М. Введение в геометрию. – М.: Наука, 1966.
    7. Курант Р., Роббинс Г. Что такое математика? – 2-е изд. – М.: Просвещение, 1967.
    8. Прасолов В.В. Задачи по планиметрии. Часть 2. – 2-е изд. – М.: Наука, 1991.
    9. Оре О. Графы и их применение. – М.: Мир, 1965.
    10. Радемахер Г., Теплиц О. Числа и фигуры. – М.: Наука, 1966.
    11. Саркисян А.А., Колягин Ю.М. Познакомьтесь с топологией. – М.: Просвещение, 1976.
    12. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.
    13. Стюарт Ян. Концепции современной математики. – Минск: Вышэйшая школа, 1980.
    14. Харари Ф. Теория графов. – М.: Мир, 1973, с.151, с.162.
    15. Статьи из журнала //Квант.
    1971. - № 4. – С.61
    1977. - № 1. – С.60
    1974. - № 2. – С.58
    1974. - № 4. – С.23
    1972. - № 4. – С.30
    16. Журнал //Наука и жизнь. – 1979. - № 3. – С.80.